Backtracking is a general algorithm for finding all (or some) solutions to some computational problems (notably Constraint satisfaction problems or CSPs), which incrementally builds candidates to the solution and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot lead to a valid solution
Category: Interview
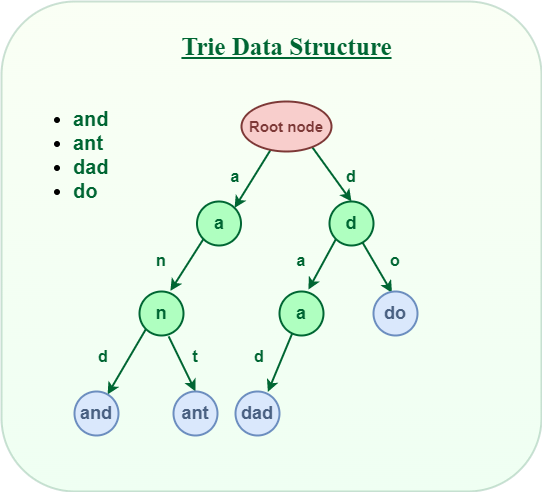
Trie
Index
- Definition
- Time-Complexity
- Programmatic representation
- Operations
- Insertion
- Search/Auto-completion
Definition
- Trie comes from word reTrieval.
- Trie is a k-way tree DS.
- It is optimised for retrieval where string have common prefix which are store on common nodes.
Time Complexity
- It has time complexity of O(N) where N is the maximum length of string.
Programmatic representation
- A Node is represented as class having 2 things –
- children representing one of 26 characters for a node.
- isLastNode – representing last node of string.
class TrieNode{
//representing one of 26 characters of alphabet for a node
TrieNode children;
//representing last node of string.
boolean isLastNode;
TrieNode(){
children=new TrieNode[26];
isLastNode=false;
}
}
Trie Operation and applications:
Insertion :
class TrieNode{
TrieNode children;
boolean isLastNode;
TrieNode(){
children=new TrieNode[26];
isLastNode=false;
}
}
Class Trie{
TrieNode root;
Trie(){
root=new TrieNode();
}
public static void main(){
Trie trie=new Trie;
trie.insert("parag");
trie.insert("parameter");
trie.insert("parashoot");
trie.autocomplete("para");
}
private void insert(String word){
TrieNode current=root;
}
private void autoComplete(String prefix){
TrieNode current=root;
}
}
Recursion
Objectives
- Significance
- Flow of control
- Memory usage
- Interview FAQs
Recursion is a process by which a function or a method calls itself again and again. Analogy: Anything that can be done in for loop can be done by recursion
Iteration VS Recursion
| Criteria | Recursion | Iteration |
|---|---|---|
| Definition | Recursion is a process where a method calls itself repeatedly until a base condition is met. | Iteration is a process by which a piece of code is repeatedly executed for a finite number of times or until a condition is met. |
| Applicability | Is the application for functions. | Is applicable for loops. |
| Chunk of code can be applied to? | Works well for smaller code size. | Works well for larger code size. |
| Memory Footprint | Utilizes more memory as each recursive call is pushed to the stack | Comparatively less memory is used. |
| Maintainability | Difficult to debug and maintain | Easier to debug and maintain |
| Type of errors expected | Results in stack overflow if the base condition is not specified or not reached | May execute infinitely but will ultimately stop execution with any memory errors |
| Time-Complexity | Time complexity is very high. | Time complexity is relatively on the lower side. |
Structure : Any method that implements Recursion has two basic parts:
- Method call which can call itself i.e. recursive
- A precondition that will stop the recursion.
Note that a precondition is necessary for any recursive method as, if we do not break the recursion then it will keep on running infinitely and result in a stack overflow.
Syntax- The general syntax of recursion is as follows:
methodName (T parameters…)
{
if (precondition == true)
//precondition or base condition
{
return result;
}
return methodName (T parameters…);
//recursive call
}
Associated Error – Stack Overflow Error In Recursion
We are aware that when any method or function is called, the state of the function is stored on the stack and is retrieved when the function returns. The stack is used for the recursive method as well.
But in the case of recursion, a problem might occur if we do not define the base condition or when the base condition is somehow not reached or executed. If this situation occurs then the stack overflow may arise.
Types of recursion
- Tail Recursion
- Head Recursion
- Tree recursion
Tail Recursion
When the call to the recursive method is the last statement executed inside the recursive method, it is called “Tail Recursion”.
In tail recursion, the recursive call statement is usually executed along with the return statement of the method.
methodName ( T parameters…){
{
if (base_condition == true)
{
return result;
}
return methodName (T parameters …) //tail recursion
}
Head Recursion
Head recursion is any recursive approach that is not a tail recursion. So even general recursion is ahead recursion.
methodName (T parameters…){
if (some_condition == true)
{
return methodName (T parameters…);
}
return result;
}
Tree Recursion
Has two recursive calls(Left/right sub-tree)
Problem-Solving Using Recursion
The basic idea behind using recursion is to express the bigger problem in terms of smaller problems. Also, we need to add one or more base conditions so that we can come out of recursion.
PAGE BREAK
FAQS
Q #1.How does Recursion work in Java?
Answer: In recursion, the recursive function calls itself repeatedly until a base condition is satisfied. The memory for the called function is pushed on to the stack at the top of the memory for the calling function. For each function call, a separate copy of local variables is made.
Q #2) Why is Recursion used?
Answer: Recursion is used to solve those problems that can be broken down into smaller ones and the entire problem can be expressed in terms of a smaller problem.
Recursion is also used for those problems that are too complex to be solved using an iterative approach. Besides the problems for which time complexity is not an issue, use recursion.
Q #3) What are the benefits of Recursion?
Answer:
The benefits of Recursion include:
- Recursion reduces redundant calling of function.
- Recursion allows us to solve problems easily when compared to the iterative approach.
Q #4) Which one is better – Recursion or Iteration?
Answer: Recursion makes repeated calls until the base function is reached. Thus there is a memory overhead as a memory for each function call is pushed on to the stack.
Iteration on the other hand does not have much memory overhead. Recursion execution is slower than the iterative approach. Recursion reduces the size of the code while the iterative approach makes the code large.
Recursion is better than the iterative approach for problems like the Tower of Hanoi, tree traversals, etc.

Question : how unflods while same method called:
https://leetcode.com/problems/merge-two-binary-trees/editorial/
DSA
Index
- Theory
- FAQs
A data structure is a way of organizing(defining, storing & retrieving) the data so that the data can be used efficiently.
You must about the data-structure before implementing in application to implement in a better and optimized way.
Note: This section is for
- Theoretical comparison
- Implementation of standard DS structures
(For Problem & Solution refer Competitive Programming section)
Topics :
- Introduction (& Brief Comparison)
- Array vs Array-list
- Array & String
- Array: Way to declare
- Array: ways to copy
- Array: Advantages/Applications and disadvantages
- Stack[todo]
- Queue[todo]
- List & Linked-list
- Define the Structure and add element
- traversal
- Find loop
- reverse link-list
- Mid element
- Doubly Linked-list
- Tree
- Structure
- BST -Adding nodes
- Traversal
- DFS
- In-order
- Pre-Order
- Post-Order
- BFS
- DFS
- Map
List : Array Vs Linked List
Parameters of comparison :
- Speed of accessibility
- read/search
- insert/Delete – if tied to shifting other elements ,
- storage space required
| Parameter | Array | Linked List |
|---|---|---|
| Strategy | Static in nature (shortage or wastage of memory) | dynamic in nature (grow and shrink at runtime as per need) |
| Access &Traversal | Faster as index based | Slower as required traversal to the element,node by node |
| Insertion & Removal | Require shifting (if middle element is removed or added at middle) | Fastest Insertion and Deletion |
| Unit of storage | Uses dynamically allocated node to store data. | |
| Definition | Collection of Nodes |
Frequently asked DS Question Solutions and Tips for optimization.
- Arrays Questions
- Equilibrium Index of an array
- Find row number of a binary matrix having maximum number of 1s
- Tree
- Recursion
- Head recursion
- Tail recursion
- Tree recursion
- Recursion
- Utilities
- Occurrence of each element
- Using additional DS i.e Map
- Without using additional DS
- Max Length Sub-array
- brute-force
- hash-map
- convert character to upper case
- Matrix
- properties of matrix
- related to rows and columns
- Bit-wise Operation
- Single iteration find non-duplicate(XOR)
- Occurrence of each element
MFA questions
Asymptotic Analysis and notation
Index
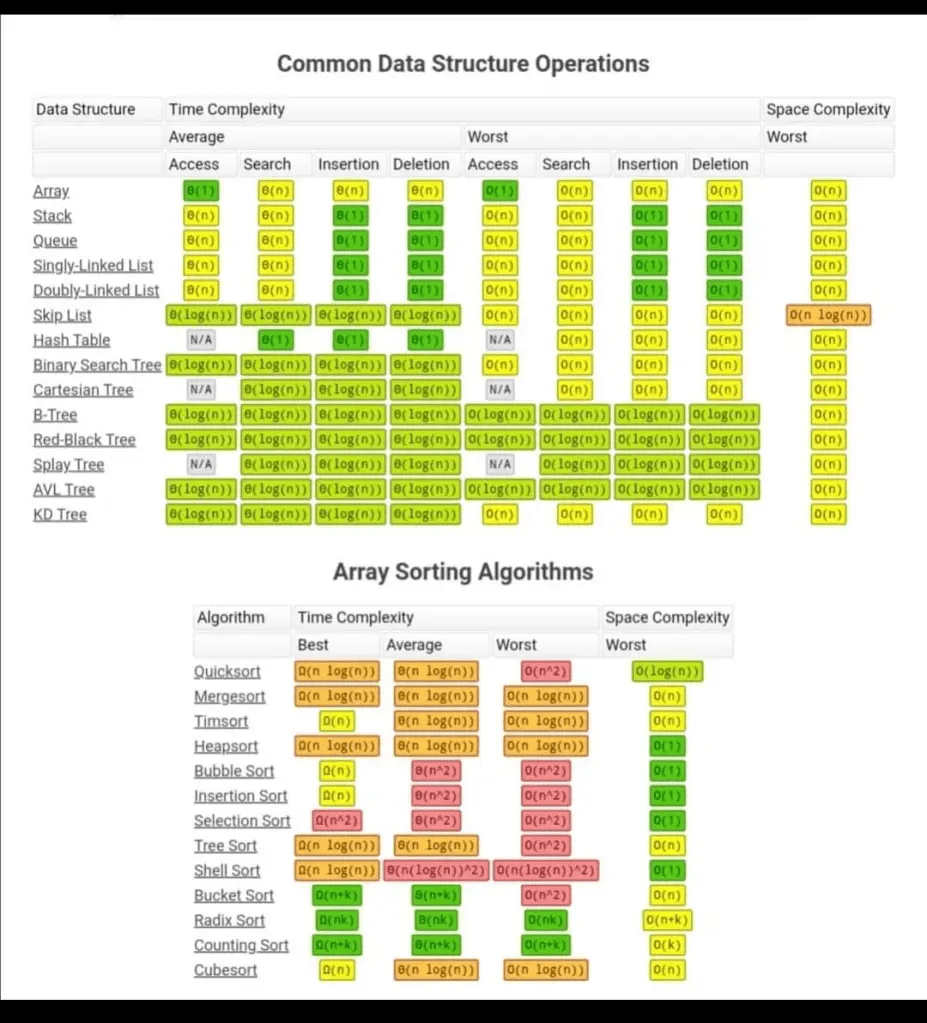
- Time Complexity
- Common DS Operations Time Complexity and Space Complexity
Time-complexity
Big-O notation: 𝑂O
It describes the asymptotic upper bound, the worst case of time complexity. i.e the max number of times a statement executes.
Measurement of time complexity
- O(N) Linear TC – When the number of operation growth is proportional to input i.e same number of operation as the input size then it’s Linear TC
- O(N^2) – Quadratic Algorithm TC
- O(LogN) -when algorithm decreases the input data in each step
- Example Binary search
- O(2^n) – opeation doubles with each increment in input data.
Growth Order
O(n!) > O(2 ^n) > O(n^3) > O(n^2) > O(nlogn) > O(n) > O(Log N) > O(sqrt(N)) > 1
Graph
Index
- Introduction
- Dijkstra Algorithm
- Bellman-ford Algorithm
- Floyd-Warshall Algorithm
- Prim’s Algorithm
Introduction
Common Terminology –
- Minimum Spanning Tree (MST) used in prims algorithm
- Goal: To connect all vertices in a graph with the minimum possible total edge weight, without forming any cycles.
- Output: A tree that spans all vertices of the graph with the minimum sum of edge weights.
- Shortest path
- Goal: To find the shortest path between a specific pair of vertices in a graph, minimizing the sum of the edge weights along that path.
- Output: A path (which may include some or all vertices) with the minimum possible total weight between two specific vertices.
Dijkstra Algorithm
- Purpose: Finds the shortest path from a single source to all other vertices in a graph.
- Applicability: Works only with graphs that have non-negative edge weights.
- Woking:
- Uses a greedy approach.
- Iteratively selects the vertex with the smallest known distance, explores its neighbors, and updates their distances.
- Once a vertex is processed, its shortest path is finalised.
Dijkstra’s algorithm is like breadth-first search (BFS), except we use a priority queue instead of a normal first-in-first-out queue. Each item’s priority is the cost of reaching it.
Note-Implementation is similar to Prim’s algorithm for minimum spanning tree.
REf-
- https://www.interviewcake.com/concept/java/dijkstras-algorithm (desciption working in chart)
- https://www.tutorialcup.com/interview/algorithm/dijkstra-algorithm.htm (application + short implemntation)
- https://www.interviewbit.com/tutorial/dijkstra-algorithm/ (Pseudo code + Graph Algo)
- https://www.interviewbit.com/tutorial/breadth-first-search/#breadth-first-search
Bellman-Ford Algorithm
- Purpose: Also finds the shortest path from a single source to all other vertices, but can handle graphs with negative edge weights.
- Applicability: Works with graphs that may have negative edge weights, and can also detect negative weight cycles (where a cycle’s total weight is negative).
- Woking:
- Uses a dynamic programming approach.
- Iteratively relaxes all edges, meaning it updates the shortest path estimate for each edge based on its current known distance.
- After V−1V-1V−1 iterations, it ensures that the shortest paths are found. If an additional relaxation improves any distance, it indicates a negative weight cycle.
Floyd-Warshall Algorithm
- Purpose: Finds the shortest paths between all pairs of vertices in a graph.
- Applicability: Works with both directed and undirected graphs, including those with negative edge weights.
- Wokings:
- Uses a dynamic programming approach.
- Iteratively updates a distance matrix where each entry
dist[i][j]represents the shortest path from vertexito vertexj. - Considers each vertex as an intermediate point in the path and updates the matrix accordingly.
Prim’s Algorithm
- Purpose: Finds the Minimum Spanning Tree (MST) of a connected, undirected graph. The MST is a subset of the edges that connects all vertices together, without any cycles, and with the minimum possible total edge weight.
- Applicability: Works with weighted, undirected graphs. It requires that the graph be connected, meaning there must be a path between every pair of vertices.
Arrays Algorithms
- Boyer-Moore Majority Voting Algorithm
- Kadane’s Algo
Boyer-Moore Majority Voting Algorithm
A majority element is one that appears more than nums.length / 2 times.
Algorithm Proceeding-
- First, choose a candidate from the given set of elements
- if it is the same as the candidate element, increase the votes. Otherwise,
- decrease the votes if votes become 0, select another new element as the new candidate.
public static int findMajorityElement(int[] nums) {
int majorityElement = 0;
int count = 0;
for (int num : nums) {
if (count == 0) {
majorityElement = num;
count = 1;
} else if (num == majorityElement) {
count++;
} else {
count--;
}
}
}
Kadane’s Algo
Kadane’s algorithm a popular dynamic programming algorithm, it is used for finding the maximum sum of a contiguous subarray in an array. it efficiently handles both positive and negative numbers.
Conditions/Cases to remember
- does it handle empty array?[NA]
- does it handle all -ve element, i.e what will be the ans in this case, since sum of 2 -ve is grater -ve number. [YES]
- should we consider using 0 or arr[i] as substitution in code – Any works ,but corresponding initiation & iteration required.
It works by maintaining two variables:maxSoFar & maxEndingHere
-
maxSoFarstores the maximum sum of any contiguous subarray seen so far, and maxEndingHerestores the maximum sum of any contiguous subarray ending at the current index.
public static int maxSubArraySum(int[] nums) {
int maxSoFar=Integer.MIN_VALUE;//final result initiated to min not 0, for cases where elements with -ve numbers would result in max being 0 -which is incorrect.
int maxEndingHere=0;
for(int i=0;i<nums.length;i++){
maxEndingHere=Math.max(nums[i]+maxEndingHere,nums[i]);
maxSoFar=Math.max(maxSoFar,maxEndingHere);
}
return maxSoFar;
}
Sorting Algorithms
Index
- Time Complexities
- Selection sort
- Bubble sort
- Insertion sort
- Quick Sort sort
- Merge Sort sort
- Heap sort
Time-Complexity of Sorting-Algorithms
| ALGORITHM | WORST-case Time Complexity(Big O Notation) | AVERAGE-case time complexity (Theta Notation) | BEST-case time-complexity (Omega Notation) |
|---|---|---|---|
| Selection sorting | O(n^2) | θ(n^2) | Ω(n^2) |
| Bubble sorting | O(n^2) | θ(n^2) | Ω(n) |
| Insertion sorting | O(n^2) | θ(n^2) | Ω(n) |
| Heap sorting | O(nlog(n)) | θ | Ω |
| Quick sorting | O(n^2) | θ | Ω |
| Merge sorting | O(nlog(n)) | θ | Ω |
| Bucket sorting | O(n^2) | θ | Ω |
| Radix sorting | O(nk) | θ | Ω |
| Tree-sort | O(nlog(n)) |
Working of Sorting Algorithms
Usage : Selection vs Insertion vs Bubble sort
- Selection Sort is best when memory write operations are costly since it makes the minimum possible number of swaps compared to other two.
- Insertion Sort is preferable for small or nearly sorted data.
- Bubble Sort is typically used for educational purposes to demonstrate sorting techniques but is rarely used in practical applications due to its inefficiency.
Selection Sorting
Algorithm :
- Iterate through the array to find the smallest (or largest) element.
- Swap the found minimum (or maximum) element with the first element.
- Move the boundary of the unsorted subarray by one element.
- Repeat the process for the remaining unsorted portion of the array.
private static void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
//optimisation used : outer loop used for swapping - internal for index tracking
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
- Time Complexity: O(n²)
- Space Complexity: O(1) (In-place sorting)
Bubble Sort
Algorithm :
- Compare adjacent elements in the array.
- Swap them if they are in the wrong order.
- Continue doing this for each pair of adjacent elements until the array is fully sorted
- .After each pass, the next largest element is in its correct position.
- Repeat the process until no swaps are needed (the array is sorted).
private static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - 1; j++) {
if(arr[j]>arr[j+1]){
int temp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
}
}
}
}
- Time Complexity: O(n²)
- Space Complexity: O(1) (In-place sorting)
Insertion Sort
Algorithm :
- Start from the second element, assume that the first element is already sorted.
- Pick the next element and compare it with the elements in the sorted part.
- Shift all elements in the sorted part that are greater than the current element to the right.
- Insert the current element into its correct position.
- Repeat the process until the entire array is sorted.
public static void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
// Move elements of arr[0..i-1] that are greater than key to one position ahead
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
- Time Complexity: O(n²)
- Space Complexity: O(1) (In-place sorting)
Quick Sort
Algorithm :
- Choose a “pivot” element from the array.
- Partition the array into two sub-arrays: elements less than the pivot and elements greater than the pivot.
- Recursively apply the same steps to the sub-arrays.
- Combine the sub-arrays to get the sorted array.
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1); // Recursively sort elements before partition
quickSort(arr, pi + 1, high); // Recursively sort elements after partition
}
}
private static int partition(int[] arr, int low, int high) {
int pivot = arr[high];
int i = (low - 1); // Index of smaller element
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
// Swap arr[i] and arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// Swap arr[i+1] and arr[high] (or pivot)
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}
- Time Complexity:
- Best Case: O(n log n)
- Worst Case: O(n²) (occurs when the smallest or largest element is always chosen as the pivot)
- Space Complexity: O(log n) (in-place sorting, though recursion stack takes
Merge Sort
Algorithm :
- Divide the array into two halves.
- Recursively sort each half.
- Merge the two halves to create a sorted array.
public class MergeSort {
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int middle = (left + right) / 2;
// Sort first and second halves
mergeSort(arr, left, middle);
mergeSort(arr, middle + 1, right);
// Merge the sorted halves
merge(arr, left, middle, right);
}
}
private static void merge(int[] arr, int left, int middle, int right) {
int n1 = middle - left + 1;
int n2 = right - middle;
// Temporary arrays
int[] L = new int[n1];
int[] R = new int[n2];
// Copy data to temp arrays
for (int i = 0; i < n1; i++)
L[i] = arr[left + i];
for (int j = 0; j < n2; j++)
R[j] = arr[middle + 1 + j];
// Merge the temp arrays
int i = 0, j = 0;
int k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// Copy remaining elements of L[]
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// Copy remaining elements of R[]
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6, 7};
// Call mergeSort with the full range of the array
mergeSort(arr, 0, arr.length - 1);
// Print the sorted array
System.out.println("Sorted array:");
for (int num : arr) {
System.out.print(num + " ");
}
}
}
Heap sort
Algorithm :
Introduction
- Asymptotic Analysis and notation
- Sorting Algorithms- nlogn
- Insertion sort
- Selection sort
- Bubble sort
- Merge SOrt
- Quick Sort
- Heap sort
- Searching Algorithms (log(n)-tree)
- Linear search
- Binary search
- DFS
- BFS
- Arrays
- Boyer-Moore Majority Voting Algorithm
- Kadane’s Algo
- Floyd’s cycle detection
- KMP
- Quick select
- Graph
- Dijkstra Algorithm
- Kruskal Algo
- Bellman ford Algo
- floyd warshall Algo
- topological sort Algo
- Flood fill Algo
- lee Algo
- Basic Algos
- Euclids Algo
- Union Find Algo
- Huffman coding compression Algo
| S.No. | Algorithm | Algorithm Design paradigm |
|---|---|---|
| 1 | Dijkstra shortest path | BFS |
| 2 | Floyd-Warshall algorithm – to compute all-pairs shortest path | Greedy design |
| 3 | Binary search on sorted array | Dynamic programming |
| 4 | Backtracking search on graph | Divide and conquer |
| 5 | DFS | |
Graph
Subset of graph is tree-which has no-loop but in graph loop is possible.
3 ways to represent Greaph
- Objects and pointers
- Matrix
- Adjacency List
Familiarise with each one of it and know the trade-offs