Category: Data Structure

Backtracking

Backtracking is a general algorithm for finding all (or some) solutions to some computational problems (notably Constraint satisfaction problems or CSPs), which incrementally builds candidates to the solution and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot lead to a valid solution

Trie

Index

  1. Definition
  2. Time-Complexity
  3. Programmatic representation
  4. Operations
    1. Insertion
    2. Search/Auto-completion

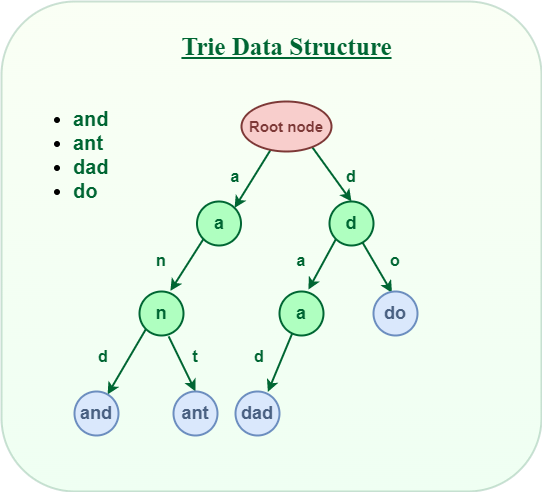
Definition

  1. Trie comes from word reTrieval.
  2. Trie is a k-way tree DS.
  3. It is optimised for retrieval where string have common prefix which are store on common nodes.

Time Complexity

  1. It has time complexity of O(N) where N is the maximum length of string.

Programmatic representation

  1. A Node is represented as class having 2 things –
    1. children representing one of 26 characters for a node.
    2. isLastNode – representing last node of string.

class TrieNode{
//representing one of 26 characters of alphabet for a node
TrieNode children;
//representing last node of string.
boolean isLastNode;
TrieNode(){
children=new TrieNode[26];
isLastNode=false;
}
}

Trie Operation and applications:

Insertion : 

class TrieNode{

TrieNode children;
boolean isLastNode;

TrieNode(){
children=new TrieNode[26];
isLastNode=false;
}

}

Class Trie{
TrieNode root;
Trie(){
root=new TrieNode();
}


public static void main(){
Trie trie=new Trie;
trie.insert("parag");
trie.insert("parameter");
trie.insert("parashoot");
trie.autocomplete("para");
}
private void insert(String word){
TrieNode current=root;
}
private void autoComplete(String prefix){
TrieNode current=root;
}
}

Recursion

Objectives

  1. Significance
  2. Flow of control
  3. Memory usage
  4. Interview FAQs

Recursion is a process by which a function or a method calls itself again and again. Analogy: Anything that can be done in for loop can be done by recursion

Iteration VS Recursion

CriteriaRecursionIteration
DefinitionRecursion is a process where a method calls itself repeatedly until a base condition is met.Iteration is a process by which a piece of code is repeatedly executed for a finite number of times or until a condition is met.
ApplicabilityIs the application for functions.Is applicable for loops.
Chunk of code can be applied to?Works well for smaller code size.Works well for larger code size.
Memory FootprintUtilizes more memory as each recursive call is pushed to the stackComparatively less memory is used.
MaintainabilityDifficult to debug and maintainEasier to debug and maintain
Type of errors expectedResults in stack overflow if the base condition is not specified or not reachedMay execute infinitely but will ultimately stop execution with any memory errors
Time-ComplexityTime complexity is very high.Time complexity is relatively on the lower side.





Structure : Any method that implements Recursion has two basic parts:

  1. Method call which can call itself i.e. recursive
  2. A precondition that will stop the recursion.

Note that a precondition is necessary for any recursive method as, if we do not break the recursion then it will keep on running infinitely and result in a stack overflow.

Syntax- The general syntax of recursion is as follows:

methodName (T parameters…)
{   
    if (precondition == true)
//precondition or base condition
    {
        return result;
    }
    return methodName (T parameters…);
 
        //recursive call
}

Associated Error – Stack Overflow Error In Recursion

We are aware that when any method or function is called, the state of the function is stored on the stack and is retrieved when the function returns. The stack is used for the recursive method as well.

But in the case of recursion, a problem might occur if we do not define the base condition or when the base condition is somehow not reached or executed. If this situation occurs then the stack overflow may arise.

Types of recursion

  1. Tail Recursion
  2. Head Recursion
  3. Tree recursion

Tail Recursion

When the call to the recursive method is the last statement executed inside the recursive method, it is called “Tail Recursion”.

In tail recursion, the recursive call statement is usually executed along with the return statement of the method.

methodName ( T parameters…){
{   
    if (base_condition == true)
    {
        return result;
    }
    return methodName (T parameters …)      //tail recursion
}

Head Recursion

Head recursion is any recursive approach that is not a tail recursion. So even general recursion is ahead recursion.

methodName (T parameters…){
    if (some_condition == true)
    {
        return methodName (T parameters…);
    }
    return result;
}

Tree Recursion

Has two recursive calls(Left/right sub-tree)

Problem-Solving Using Recursion

The basic idea behind using recursion is to express the bigger problem in terms of smaller problems. Also, we need to add one or more base conditions so that we can come out of recursion.

PAGE BREAK

FAQS

Q #1.How does Recursion work in Java?

Answer: In recursion, the recursive function calls itself repeatedly until a base condition is satisfied. The memory for the called function is pushed on to the stack at the top of the memory for the calling function. For each function call, a separate copy of local variables is made.

Q #2) Why is Recursion used?

Answer: Recursion is used to solve those problems that can be broken down into smaller ones and the entire problem can be expressed in terms of a smaller problem.

Recursion is also used for those problems that are too complex to be solved using an iterative approach. Besides the problems for which time complexity is not an issue, use recursion.

Q #3) What are the benefits of Recursion?

Answer:

The benefits of Recursion include:

  1. Recursion reduces redundant calling of function.
  2. Recursion allows us to solve problems easily when compared to the iterative approach.

Q #4) Which one is better – Recursion or Iteration?

Answer: Recursion makes repeated calls until the base function is reached. Thus there is a memory overhead as a memory for each function call is pushed on to the stack.

Iteration on the other hand does not have much memory overhead. Recursion execution is slower than the iterative approach. Recursion reduces the size of the code while the iterative approach makes the code large.

Recursion is better than the iterative approach for problems like the Tower of Hanoi, tree traversals, etc.

Finding the factorial of a number using recursion
Factorial Recursive call

Question : how unflods while same method called:

https://leetcode.com/problems/merge-two-binary-trees/editorial/

DSA

Index

  • Theory
  • FAQs

A data structure is a way of organizing(defining, storing & retrieving) the data so that the data can be used efficiently.

You must about the data-structure before implementing in application to implement in a better and optimized way.

Note: This section is for

  1. Theoretical comparison
  2. Implementation of standard DS structures

(For Problem & Solution refer Competitive Programming section)

Topics :

  1. Introduction (& Brief Comparison)
    • Array vs Array-list
  2. Array & String
    1. Array: Way to declare
    2. Array: ways to copy
    3. Array: Advantages/Applications and disadvantages
  3. Stack[todo]
  4. Queue[todo]
  5. List & Linked-list
    1. Define the Structure and add element
    2. traversal
    3. Find loop
    4. reverse link-list
    5. Mid element
    6. Doubly Linked-list
  6. Tree
    1. Structure
    2. BST -Adding nodes
    3. Traversal
      1. DFS
        • In-order
        • Pre-Order
        • Post-Order
      2. BFS
  7. Map

List : Array Vs Linked List

Parameters of comparison :

  1. Speed of accessibility
    1. read/search
    2. insert/Delete – if tied to shifting other elements ,
  2. storage space required
ParameterArrayLinked List
StrategyStatic in nature (shortage or wastage of memory)dynamic in nature (grow and shrink at runtime as per need)
Access &TraversalFaster as index basedSlower as required traversal to the element,node by node
Insertion & RemovalRequire shifting (if middle element
is removed or added at middle)		Fastest Insertion and Deletion
Unit of storageUses dynamically allocated node to store data.
DefinitionCollection of Nodes

Frequently asked DS Question Solutions and Tips for optimization.

  1. Arrays Questions
    • Equilibrium Index of an array
    • Find row number of a binary matrix having maximum number of 1s
  2. Tree
    • Recursion
      1. Head recursion
      2. Tail recursion
      3. Tree recursion
  3. Utilities
    1. Occurrence of each element
      • Using additional DS i.e Map
      • Without using additional DS
    2. Max Length Sub-array
      • brute-force
      • hash-map
    3. convert character to upper case
    4. Matrix
      • properties of matrix
      • related to rows and columns
    5. Bit-wise Operation
      • Single iteration find non-duplicate(XOR)

MFA questions

https://www.linkedin.com/posts/kartikey-sapra_i-spent-4-hours-to-collect-the-links-of-activity-7198365904563286016-T_Hf/?utm_source=share&utm_medium=member_android

Dynamic Programming

Index

  1. Introduction to Dynamic Programming
    1. Strategic Approach
    2. Common patterns
      • Top-Down Approach – recursion+memorisation
      • Bottom-up Approach – tabulation.

Introduction to Dynamic Programming

What is Dynamic Programming?

Dynamic Programming (DP) is a programming paradigm that can systematically and efficiently explore all possible solutions to a problem. As such, it is capable of solving a wide variety of problems that often have the following characteristics:

  1. The problem can be broken down into “overlapping subproblems” – smaller versions of the original problem that are re-used multiple times.
  2. The problem has an “optimal substructure” – an optimal solution can be formed from optimal solutions to the overlapping subproblems of the original problem.

Fibonacci Example –

If you wanted to find the n^{th}nth Fibonacci number F(n)F(n), you can break it down into smaller subproblems – find F(n – 1)F(n−1) and F(n – 2)F(n−2) instead. Then, adding the solutions to these subproblems together gives the answer to the original question, F(n – 1) + F(n – 2) = F(n)F(n−1)+F(n−2)=F(n), which means the problem has optimal substructure, since a solution F(n)F(n) to the original problem can be formed from the solutions to the subproblems. These subproblems are also overlapping – for example, we would need F(4)F(4) to calculate both F(5)F(5) and F(6)F(6).

These attributes may seem familiar to you. Greedy problems have optimal substructure, but not overlapping subproblems. Divide and conquer algorithms break a problem into subproblems, but these subproblems are not overlapping (which is why DP and divide and conquer are commonly mistaken for one another).

There are two ways to implement a DP algorithm:

  1. Bottom-up, also known as tabulation.
  2. Top-down, also known as memoization.

Bottom-up (Tabulation)

Bottom-up is implemented with iteration and starts at the base cases. Let’s use the Fibonacci sequence as an example again. The base cases for the Fibonacci sequence are F(0)=0 and F(1) = 1. With bottom-up, we would use these base cases to calculate F(2)F(2), and then use that result to calculate F(3), and so on all the way up to F(n)

Pseudi COde 

// Pseudocode example for bottom-up

F = array of length (n + 1)
F[0] = 0
F[1] = 1
for i from 2 to n:
    F[i] = F[i - 1] + F[i - 2]

Top-down (Memoization)

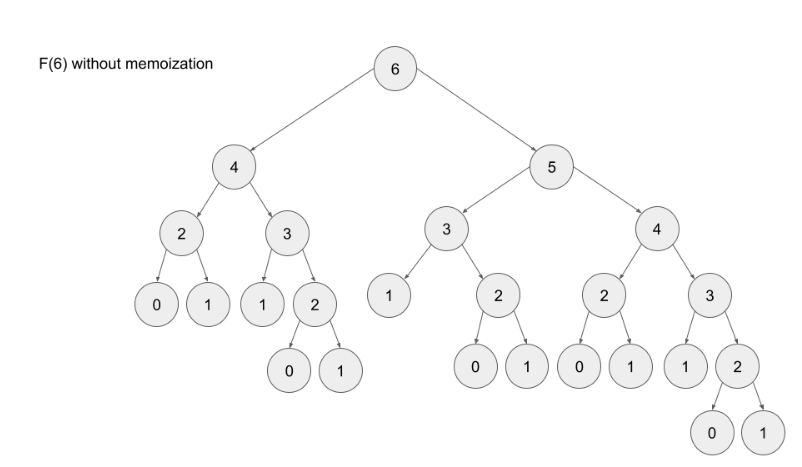
Top-down is implemented with recursion and made efficient with memoization. If we wanted to find the n^{th}nth Fibonacci number F(n)F(n), we try to compute this by finding F(n – 1)F(n−1) and F(n – 2)F(n−2). This defines a recursive pattern that will continue on until we reach the base cases F(0) = F(1) = 1F(0)=F(1)=1. The problem with just implementing it recursively is that there is a ton of unnecessary repeated computation. Take a look at the recursion tree if we were to find F(5)F(5):

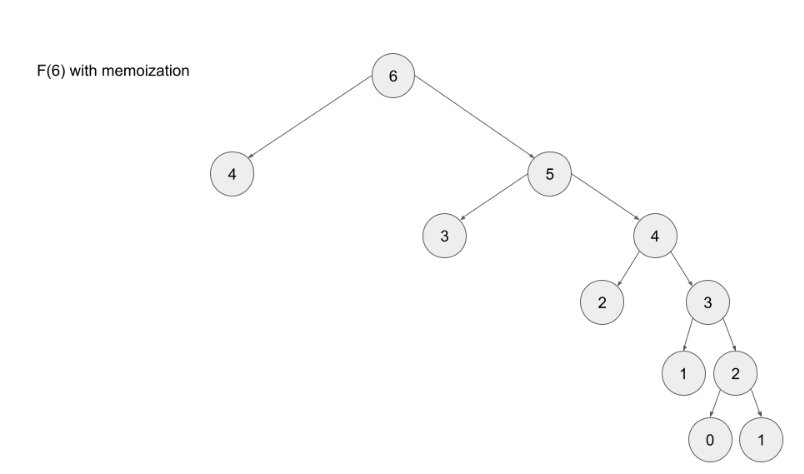
Notice that we need to calculate F(2) three times. This might not seem like a big deal, but if we were to calculate F(6), this entire image would be only one child of the root. Imagine if we wanted to find F(100) – the amount of computation is exponential and will quickly explode. The solution to this is to memoize results.

Note- memoizing a result means to store the result of a function call, usually in a hashmap or an array, so that when the same function call is made again, we can simply return the memoized result instead of recalculating the result.

memorisation vs without memorisation

Advantages

  • It is very easy to understand and implement.
  • It solves the subproblems only when it is required.
  • It is easy to debug.

Disadvantages

  • It uses the recursion technique that occupies more memory in the call stack.
  • Sometimes when the recursion is too deep, the stack overflow condition will occur.
  • It occupies more memory that degrades the overall performance.

When to Use DP

Following are the scenarios to use DP-

  1. The problem can be broken down into “overlapping subproblems” – smaller versions of the original problem that are re-used multiple times
  2. The problem has an “optimal substructure” – an optimal solution can be formed from optimal solutions to the overlapping subproblems of the original problem.

Unfortunately, it is hard to identify when a problem fits into these definitions. Instead, let’s discuss some common characteristics of DP problems that are easy to identify.

The first characteristic that is common in DP problems is that the problem will ask for the optimum value (maximum or minimum) of something, or the number of ways there are to do something. For example:

  • Optimization problems.
    • What is the minimum cost of doing…
    • What is the maximum profit from…
    • How many ways are there to do…
    • What is the longest possible…
    • Is it possible to reach a certain point…
  • Combinatorial problems.
    • given a number N, you’ve to find the number of different ways to write it as the sum of 1, 3 and 4.

Note: Not all DP problems follow this format, and not all problems that follow these formats should be solved using DP. However, these formats are very common for DP problems and are generally a hint that you should consider using dynamic programming.

When it comes to identifying if a problem should be solved with DP, this first characteristic is not sufficient. Sometimes, a problem in this format (asking for the max/min/longest etc.) is meant to be solved with a greedy algorithm. The next characteristic will help us determine whether a problem should be solved using a greedy algorithm or dynamic programming.

The second characteristic that is common in DP problems is that future “decisions” depend on earlier decisions. Deciding to do something at one step may affect the ability to do something in a later step. This characteristic is what makes a greedy algorithm invalid for a DP problem – we need to factor in results from previous decisions.

Algorithm –

You can either use Map or array to store/memoize the elements (both gives O(1) access time.

Tree

It’s a recursive(/Iterative) DS

Index

  1. Tree Theory
    1. Introduction
    1. Binary Tree
      1. Search- (tc -O(n) same reason as BST)
    2. Binary Search Tree
      1. Inserting node (tc -O(n) -if emenents are skewed one sided (left/right)-need to traversed the all nodes i.e height of tree to insert)
      2. Searching for a node (tc -O(n))
      3. Questions
  2. Tree Implementation
    1. Node representation
    2. Inserting node in BST
    3. Tree-traversal
      1. DFS
        1. Recursively (hard to explain in case of backtracking)
        2. Iteratively (using stack)
        3. Questions
      2. BFS
        1. Iteratively (using queue)
        2. Questions
    4. Expression tree & Binary Tree

Topics Covered-

  1. Definition & Components of tree
  2. Where to use?
  3. Denoting Tree in Java
  4. Types of Tree
  5. Traversal and searching

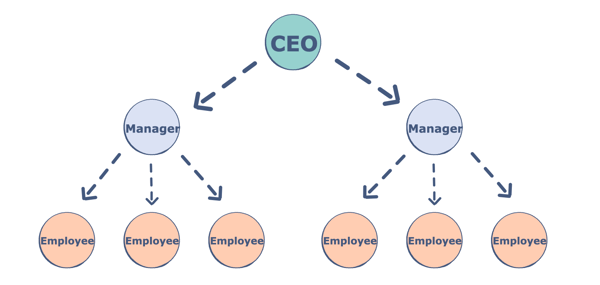
Trees are non-linear data structures. They are often used to represent hierarchical data. For a real-world example, a hierarchical company structure uses a tree to organize.

Tree have 1:N parent-child relation, if N is 2 then we call it Binary Tree

widget

Components of a Tree

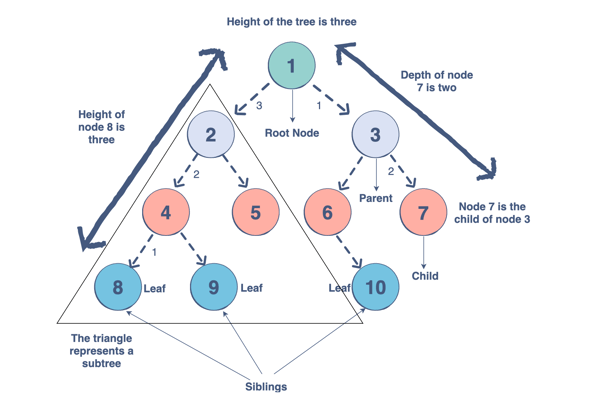
Trees are a collection of nodes (vertices), and they are linked with edges (pointers), representing the hierarchical connections between the nodes. A node contains data of any type, but all the nodes must be of the same data type. Trees are similar to graphs, but a cycle cannot exist in a tree. What are the different components of a tree?

  1. Root: The root of a tree is a node that has no incoming link (i.e. no parent node). Think of this as a starting point of your tree.
  2. Children: The child of a tree is a node with one incoming link from a node above it (i.e. a parent node). If two children nodes share the same parent, they are called siblings.
  3. Parent: The parent node has an outgoing link connecting it to one or more child nodes
  4. Leaf: A leaf has a parent node but has no outgoing link to a child node. Think of this as an endpoint of your tree.
  5. Subtree: A subtree is a smaller tree held within a larger tree. The root of that tree can be any node from the bigger tree.
  6. Depth: The depth of a node is the number of edges between that node and the root. Think of this as how many steps there are between your node and the tree’s starting point.
  7. Height: The height of a node is the number of edges in the longest path from a node to a leaf node. Think of this as how many steps there are between your node and the tree’s endpoint. The height of a tree is the height of its root node.
  8. Degree: The degree of a node refers to the number of sub-trees.
widget

Why do we use trees?

The hierarchical structure gives a tree unique properties for storing, manipulating, and accessing data.We can use a tree for the following:

  • Storage as hierarchy. Storing information that naturally occurs in a hierarchy. File systems on a computer and PDF use tree structures.
  • Searching. Storing information that we want to search quickly. Trees are easier to search than a Linked List. Some types of trees (like AVL and Red-Black trees) are designed for fast searching.
  • Inheritance. Trees are used for inheritance, XML parser, machine learning, and DNS, amongst many other things.
  • Indexing. Advanced types of trees, like B-Trees and B+ Trees, can be used for indexing a database.
  • Networking. Trees are ideal for things like social networking and computer chess games.
  • Shortest path. A Spanning Tree can be used to find the shortest paths in routers for networking.

How to make a tree/?

To build a tree in Java we start with the root node.

Node<String> root = new Node<>("root");

Once we have our root, we can add our first child node using addChild, which adds a child node and assigns it to a parent node. We refer to this process as insertion (adding nodes) and deletion (removing nodes)

Node<String> node1 = root.addChild(new Node<String>("node 1"));

Types of Trees

There are many types of trees that we can use to organize data differently within a hierarchical structure.The tree we use depends on the problem we are trying to solve. Let’s take a look at the trees we can use in Java. We will be covering:

  1. N-ary trees
  2. Balanced trees
  3. Binary trees
  4. Binary Search Trees
  5. AVL Trees
  6. Red-Black Trees
  7. 2-3 Trees
  8. 2-3-4 Trees

There are 3 main types of Binary tree based on thier structureL

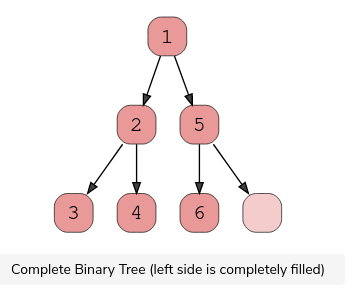
1.Complete Binary Tree

A complete binary tree exists when every level, excluding the last, is filled and all nodes at the last level are as far left as they can be. Here is a visual representation of a complete binary tree.

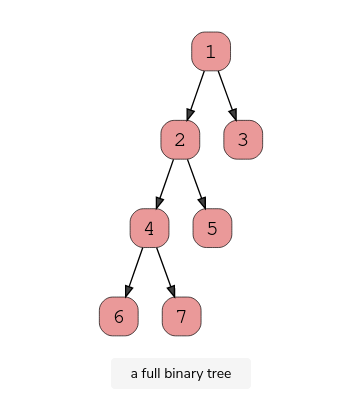
2.Full Binary Tree

A full binary tree (sometimes called proper binary tree) exits when every node, excluding the leaves, has two children. Every level must be filled, and the nodes are as far left as possible. Look at this diagram to understand how a full binary tree looks.

3.Perfect Binary Tree

A perfect binary tree should be both full and complete. All interior nodes should have two children, and all leaves must have the same depth. Look at this diagram to understand how a perfect binary tree looks.

A perfect binary tree should be both full and complete. All interior nodes should have two children, and all leaves must have the same depth. Look at this diagram to understand how a perfect binary tree looks.

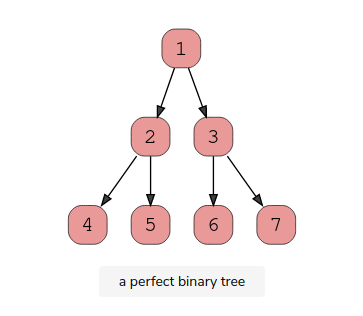
Binary Search Trees

A Binary Search Tree is a binary tree in which every node has a key and an associated value. This allows for quick lookup and edits (additions or removals), hence the name “search”.

It’s important to note that every Binary Search Tree is a binary tree, but not every binary tree is a Binary Search Tree.

What makes them different? In a Binary Search Tree, the left subtree of a subtree must contain nodes with fewer(smaller) keys than a node’s key, while the right subtree will contain nodes with keys greater than that node’s key. Take a look at this visual to understand this condition.

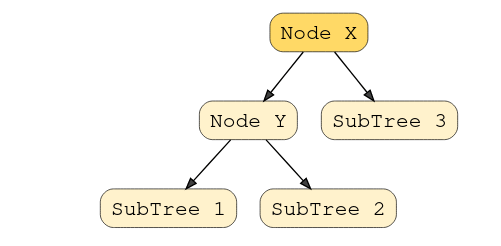
In this example, the node Y is a parent node with two child nodes. All nodes in subtree 1 must have a value less than node Y, and subtree 2 must have a greater value than node Y.

Red Black Tree (Used in HashMap Java-8)

Intro to Tree Traversal and Searching

To use trees, we can traverse them by visiting/checking every node of a tree. If a tree is “traversed”, this means every node has been visited. There are four ways to traverse a tree. These four processes fall into one of two categories: breadth-first traversal or depth-first traversal.

Note : the traversal technique – in-order, pre-order and post-order only applies to binary tree where as DFS (iteratively using stack)can also be used for general graph for traversal.

  1. DFS 3 OPTIONS (Position of root node)-
    • In-order ,
    • post-order (for deleting nodes),
    • preorder (preorder expression)
  2. BFS – one- option
    • Level order
  1. In-order Traversal –
    1. as the name suggests gives the sorted number [in ascending order]
    2. Think of this as moving up the tree, then back down. You traverse the left child and its sub-tree until you reach the root. Then, traverse down the right child and its subtree. This is a depth-first traversal.
    3. Manual traversal hind- take the traversal order (LrR)–>1st one to print is L sub-tree(take the L sub tree as a tree and apply LrR)
  2. Pre-order Traversal –
    1. Helps in creating the copy of the tree.Preorder traversal is also used to get prefix expression on of an expression tree.
    2. This of this as starting at the top, moving down, and then over. You start at the root, traverse the left sub-tree, and then move over to the right sub-tree. This is a depth-first traversal.
    3. Manual traversal hind- take the traversal order (rLR)–>1st one to print is L sub-tree(take the L sub tree as a tree and apply rLR)
  3. Post-order Traversal –
    1. Aids in deletion of nodes as it traverses the child nodes first and then the root node..so helps avoid orphan node while deleting nodes .Postorder traversal is also useful to get the postfix expression of an expression tree.
    2. Begin with the left-sub tree and move over to the right sub-tree. Then, move up to visit the root node. This is a depth-first traversal
  4. Levelorder: Think of this as a sort of zig-zag pattern. This will traverse the nodes by their levels instead of subtrees. First, we visit the root and visit all children of that root, left to right. We then move down to the next level until we reach a node that has no children. This is the left node. This is a breadth-first traversal.

Depth First Search/Traversal

Overview: We follow a path from the starting node to the ending node and then start another path until all nodes are visited. This is commonly implemented using stacks, and it requires less memory than BFS. It is best for topographical sorting, such as graph backtracking or cycle detection.

The steps for the DFS algorithm are as follows:

  1. Pick a node. Push all adjacent nodes into a stack.
  2. Pop a node from that stack and push adjacent nodes into another stack.
  3. Repeat until the stack is empty or you have reached your goal. As you visit nodes, you must mark them as visited before proceeding, or you will be stuck in an infinite loop.

BFS traversal -Level Order Traversal

Overview: We proceed level-by-level to visit all nodes at one level before going to the next. The BFS algorithm is commonly implemented using queues, and it requires more memory than the DFS algorithm. It is best for finding the shortest path between two nodes.

The steps for the BFS algorithm are as follows:

  1. Pick a node. Enqueue all adjacent nodes into a queue. Dequeue a node, and mark it as visited. Enqueue all adjacent nodes into another queue.
  2. Repeat until the queue is empty of you have met your goal.
  3. As you visit nodes, you must mark them as visited before proceeding, or you will be stuck in an infinite loop.

Application/Uses of Tree traversal – BFS traversal Application

  1. Copying Garbage Collection,Cheney’s Algorithm
  2. Finding shortest path between two nodes
  3. Minimum spanning tree

Pages: Page 1, Page 2