Graph – Techglot

It’s a recursive(/Iterative) DS

Index

Tree Theory
1. Introduction
1. Binary Tree
  1. Search- (tc -O(n) same reason as BST)
2. Binary Search Tree
  1. Inserting node (tc -O(n) -if emenents are skewed one sided (left/right)-need to traversed the all nodes i.e height of tree to insert)
  2. Searching for a node (tc -O(n))
  3. Questions
Tree Implementation
1. Node representation
2. Inserting node in BST
3. Tree-traversal
  1. DFS
    1. Recursively (hard to explain in case of backtracking)
    2. Iteratively (using stack)
    3. Questions
  2. BFS
    1. Iteratively (using queue)
    2. Questions
4. Expression tree & Binary Tree

Topics Covered-

Definition & Components of tree
Where to use?
Denoting Tree in Java
Types of Tree
Traversal and searching

Trees are non-linear data structures. They are often used to represent hierarchical data. For a real-world example, a hierarchical company structure uses a tree to organize.

Tree have 1:N parent-child relation, if N is 2 then we call it Binary Tree

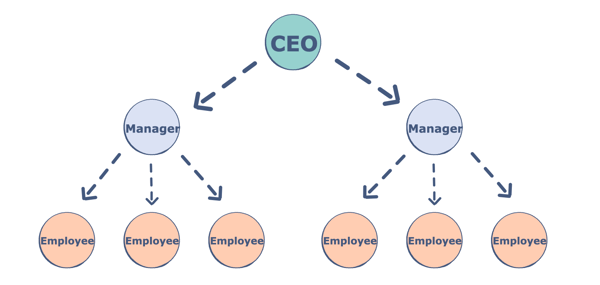
Components of a Tree

Trees are a collection of nodes (vertices), and they are linked with edges (pointers), representing the hierarchical connections between the nodes. A node contains data of any type, but all the nodes must be of the same data type. Trees are similar to graphs, but a cycle cannot exist in a tree. What are the different components of a tree?

Root: The root of a tree is a node that has no incoming link (i.e. no parent node). Think of this as a starting point of your tree.
Children: The child of a tree is a node with one incoming link from a node above it (i.e. a parent node). If two children nodes share the same parent, they are called siblings.
Parent: The parent node has an outgoing link connecting it to one or more child nodes
Leaf: A leaf has a parent node but has no outgoing link to a child node. Think of this as an endpoint of your tree.
Subtree: A subtree is a smaller tree held within a larger tree. The root of that tree can be any node from the bigger tree.
Depth: The depth of a node is the number of edges between that node and the root. Think of this as how many steps there are between your node and the tree’s starting point.
Height: The height of a node is the number of edges in the longest path from a node to a leaf node. Think of this as how many steps there are between your node and the tree’s endpoint. The height of a tree is the height of its root node.
Degree: The degree of a node refers to the number of sub-trees.

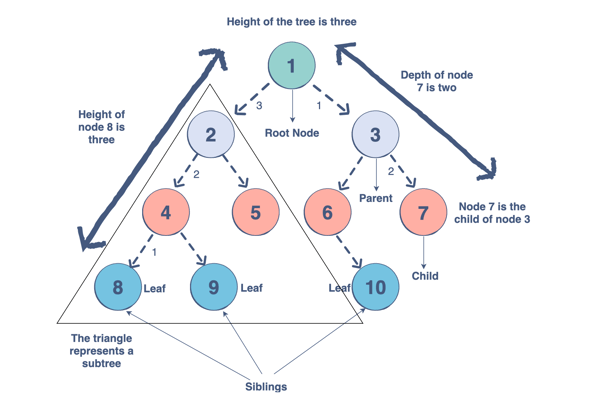
Why do we use trees?

The hierarchical structure gives a tree unique properties for storing, manipulating, and accessing data.We can use a tree for the following:

Storage as hierarchy. Storing information that naturally occurs in a hierarchy. File systems on a computer and PDF use tree structures.
Searching. Storing information that we want to search quickly. Trees are easier to search than a Linked List. Some types of trees (like AVL and Red-Black trees) are designed for fast searching.
Inheritance. Trees are used for inheritance, XML parser, machine learning, and DNS, amongst many other things.
Indexing. Advanced types of trees, like B-Trees and B+ Trees, can be used for indexing a database.
Networking. Trees are ideal for things like social networking and computer chess games.
Shortest path. A Spanning Tree can be used to find the shortest paths in routers for networking.

How to make a tree/?

To build a tree in Java we start with the root node.

Node<String> root = new Node<>("root");

Once we have our root, we can add our first child node using addChild, which adds a child node and assigns it to a parent node. We refer to this process as insertion (adding nodes) and deletion (removing nodes)

Node<String> node1 = root.addChild(new Node<String>("node 1"));

Types of Trees

There are many types of trees that we can use to organize data differently within a hierarchical structure.The tree we use depends on the problem we are trying to solve. Let’s take a look at the trees we can use in Java. We will be covering:

N-ary trees
Balanced trees
Binary trees
Binary Search Trees
AVL Trees
Red-Black Trees
2-3 Trees
2-3-4 Trees

There are 3 main types of Binary tree based on thier structureL

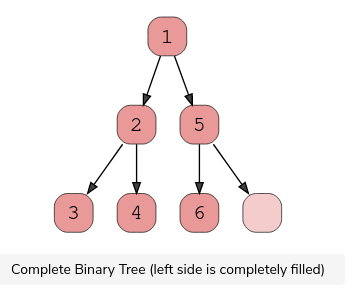
1.Complete Binary Tree

A complete binary tree exists when every level, excluding the last, is filled and all nodes at the last level are as far left as they can be. Here is a visual representation of a complete binary tree.

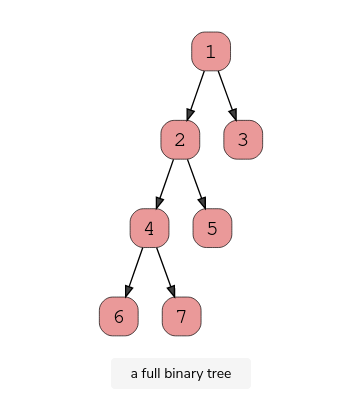
2.Full Binary Tree

A full binary tree (sometimes called proper binary tree) exits when every node, excluding the leaves, has two children. Every level must be filled, and the nodes are as far left as possible. Look at this diagram to understand how a full binary tree looks.

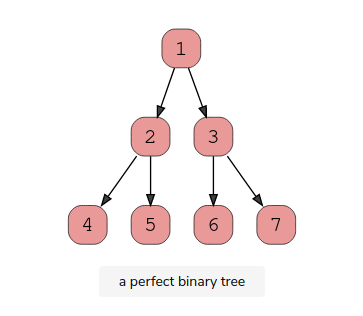
3.Perfect Binary Tree

A perfect binary tree should be both full and complete. All interior nodes should have two children, and all leaves must have the same depth. Look at this diagram to understand how a perfect binary tree looks.

Binary Search Trees

A Binary Search Tree is a binary tree in which every node has a key and an associated value. This allows for quick lookup and edits (additions or removals), hence the name “search”.

It’s important to note that every Binary Search Tree is a binary tree, but not every binary tree is a Binary Search Tree.

What makes them different? In a Binary Search Tree, the left subtree of a subtree must contain nodes with fewer(smaller) keys than a node’s key, while the right subtree will contain nodes with keys greater than that node’s key. Take a look at this visual to understand this condition.

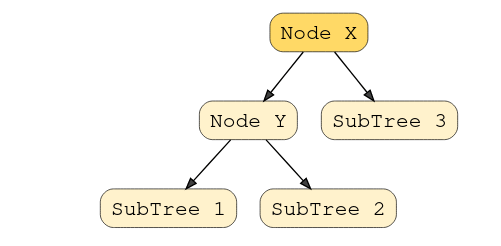
In this example, the node Y is a parent node with two child nodes. All nodes in subtree 1 must have a value less than node Y, and subtree 2 must have a greater value than node Y.

Red Black Tree (Used in HashMap Java-8)

Intro to Tree Traversal and Searching

To use trees, we can traverse them by visiting/checking every node of a tree. If a tree is “traversed”, this means every node has been visited. There are four ways to traverse a tree. These four processes fall into one of two categories: breadth-first traversal or depth-first traversal.

Note : the traversal technique – in-order, pre-order and post-order only applies to binary tree where as DFS (iteratively using stack)can also be used for general graph for traversal.

DFS 3 OPTIONS (Position of root node)-
- In-order ,
- post-order (for deleting nodes),
- preorder (preorder expression)
BFS – one- option
- Level order

In-order Traversal –
1. as the name suggests gives the sorted number [in ascending order]
2. Think of this as moving up the tree, then back down. You traverse the left child and its sub-tree until you reach the root. Then, traverse down the right child and its subtree. This is a depth-first traversal.
3. Manual traversal hind- take the traversal order (LrR)–>1st one to print is L sub-tree(take the L sub tree as a tree and apply LrR)
Pre-order Traversal –
1. Helps in creating the copy of the tree.Preorder traversal is also used to get prefix expression on of an expression tree.
2. This of this as starting at the top, moving down, and then over. You start at the root, traverse the left sub-tree, and then move over to the right sub-tree. This is a depth-first traversal.
3. Manual traversal hind- take the traversal order (rLR)–>1st one to print is L sub-tree(take the L sub tree as a tree and apply rLR)
Post-order Traversal –
1. Aids in deletion of nodes as it traverses the child nodes first and then the root node..so helps avoid orphan node while deleting nodes .Postorder traversal is also useful to get the postfix expression of an expression tree.
2. Begin with the left-sub tree and move over to the right sub-tree. Then, move up to visit the root node. This is a depth-first traversal
Levelorder: Think of this as a sort of zig-zag pattern. This will traverse the nodes by their levels instead of subtrees. First, we visit the root and visit all children of that root, left to right. We then move down to the next level until we reach a node that has no children. This is the left node. This is a breadth-first traversal.

Depth First Search/Traversal

Overview: We follow a path from the starting node to the ending node and then start another path until all nodes are visited. This is commonly implemented using stacks, and it requires less memory than BFS. It is best for topographical sorting, such as graph backtracking or cycle detection.

The steps for the DFS algorithm are as follows:

Pick a node. Push all adjacent nodes into a stack.
Pop a node from that stack and push adjacent nodes into another stack.
Repeat until the stack is empty or you have reached your goal. As you visit nodes, you must mark them as visited before proceeding, or you will be stuck in an infinite loop.

BFS traversal -Level Order Traversal

Overview: We proceed level-by-level to visit all nodes at one level before going to the next. The BFS algorithm is commonly implemented using queues, and it requires more memory than the DFS algorithm. It is best for finding the shortest path between two nodes.

The steps for the BFS algorithm are as follows:

Pick a node. Enqueue all adjacent nodes into a queue. Dequeue a node, and mark it as visited. Enqueue all adjacent nodes into another queue.
Repeat until the queue is empty of you have met your goal.
As you visit nodes, you must mark them as visited before proceeding, or you will be stuck in an infinite loop.

Application/Uses of Tree traversal – BFS traversal Application

Copying Garbage Collection,Cheney’s Algorithm
Finding shortest path between two nodes
Minimum spanning tree

Pages: 12