Tree Implementation & Application in Java
Index
- Tree Node representation
- Inserting Node in BST
- DFS
- BFS
- Questions -[CP Section] https://wordpress.com/post/techglot.tech.blog/5148
- Node Representation and Tree starting node
//Node representation
class BSTNode<T> {
T data;
BSTNode<T> left, right;
BSTNode(T val) {
//Note : T only in parameter not after Constructor name because it is itself a type
this.data = val;
left = right = null;//initiaize left and right node to null
}
}
//BST Adding Nodes in tree,smaller goes to left and greater or equal goes right
public class BinarySearchTree {
//starting node of tree i.e root
BSTNode<Integer> root ;
// Constructor with initialized reference node
BinarySearchTree(){
root=null;
}
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
System.out.println("Inorder");
inorderTraversal(root);
}
- Steps/Algo for Inserting in BST
- if the new node’s value is lower than the current node’s, we go to the left child
- if the new node’s value is greater than the current node’s, we go to the right child
- when the current node is null, we’ve reached a leaf node and we can insert the new node in that position
Code for Inserting Node in BST
// Runner code
public class BinarySearchTree {
//reference node poining to head
static BSTNode<Integer> root;
//tree initialized to null
BinarySearchTree() {
root = null;
}
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
tree.insert(5);
tree.insert(1);
}
//Recursively inserting node in BST
void insert(int key) {
root = insertREcur(root, key);// root is always pointing to first element after inserting as per logic
}
private BSTNode<Integer> insertREcur(BSTNode<Integer> current, int i) {
if (current == null) {// //base con diton
current = new BSTNode<>(i);
return current;
}
if (i < current.data) {
current.left = insertREcur(current.left, i);
} else if (i >= current.data) {
current.right = insertREcur(current.right, i);
}
return current;
}
Recursion Some programming notes
- Note1: Recursive function calls returns to the caller(i.e next line to recursive call).
- (Initially initialized variable holds the initial value after recursive calls , recursive calls are limited to its scope)
Tree Traversal – Broadly Two Ways
- DFS
- Inorder
- PreOrder
- PostOrder
Two programmatic ways of traversal for above DFS ways-
- Recursive
- Iterative
Foundation Code for traversal :
class BSTNode<T> {
T data;
BSTNode left, right;
BSTNode(T val) {
this.data = val;
left = right = null;
}
}
public class BinarySearchTree {
static BSTNode<Integer> root;
BinarySearchTree() {
root = null;
}
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
System.out.println("Inorder");
tree.inorderTraversal(root);
}
In-Order (Recursive)
private void inorderTraversal(BSTNode<Integer> root) {
if (root != null) {
inorderTraversal(root.left);//Note: it's a recursive call in all tress in all operation not just direct data right/left call
System.out.print(" --> " + root.data);
inorderTraversal(root.right);
}
}
Pre-Order (Recursive)
private static void preorderTraversal(BSTNode<Integer> root) {
if (root != null) {
System.out.print(" --> " + root.data);
preorderTraversal(root.left);
preorderTraversal(root.right);
}
}
Post-Order (Recursive)
private static void postorderTraversal(BSTNode<Integer> root) {
if (root != null) {
postorderTraversal(root.left);
postorderTraversal(root.right);
System.out.print(" --> " + root.data);
}
}
DFS Traversal – Iterative approach
- In-order-Traversal (Iterative)
- Preorder Traversal
- PostOrder Traversal
Using Stack is the obvious way to traverse tree without recursion. Below is an algorithm for traversing binary tree using stack
- Create an empty stack S.
- Initialize current node as root
- Push the current node to S and set current = current->left until current is NULL
- If current is NULL and stack is not empty then
- Pop the top item from stack.
- Print the popped item, set current = popped_item->right
- Go to step 3.
- If current is NULL and stack is empty then we are done.
1
/ \
2 3
/ \
4 5
Steps for above tree
- Step 1- Creates an empty stack: S = NULL
- Step 2 – sets current as address of root: current -> 1
- Step 3- Pushes the current node and set current = current->left ,until current is NULL
- current -> 1
- push 1: Stack S -> 1
- current -> 2
- push 2: Stack S -> 2, 1
- current -> 4
- push 4: Stack S -> 4, 2, 1
- current = NULL
- Step 4- pops from S
- Pop 2: Stack S -> 1
- print “2”
- current -> 5/*right of 2 */ and go to step 3
- Since current is NULL step 3 doesn’t do anything
- Step 4- pops again.
- Pop 1: Stack S -> NULL
- print “1”
- current -> 3 /*right of 1 */
- Step 3-pushes 3 to stack and makes current NULL
- Stack S -> 3
- current = NULL
- Step 4- pops from S
- Pop 3: Stack S -> NULL
- print “3”
- current = NULL /*right of 3 */
- Traversal is done now as stack S is empty and current is NULL.
Code
void inorder(Node root)
{
if (root == null)
return;
Stack<Node> s = new Stack<Node>();
Node curr = root;
// traverse the tree
while (curr != null || s.size() > 0)
{
/* Reach the left most Node of the
curr Node */
while (curr != null)
{
/* place pointer to a tree node on
the stack before traversing
the node's left subtree */
s.push(curr);
curr = curr.left;
}
/* Current must be NULL at this point */
curr = s.pop();
System.out.print(curr.data + " ");
/* we have visited the node and its
left subtree. Now, it's right
subtree's turn */
curr = curr.right;
}
PreOrder Traversal (DFS iterative approach using stack)
Following is a simple stack based iterative process to print Preorder traversal.
- Create an empty stack nodeStack and push root node to stack.
- Do the following while nodeStack is not empty.
- Pop an item from the stack and print it.
- Push right child of a popped item to stack
- Push left child of a popped item to stack
- The right child is pushed before the left child to make sure that the left subtree is processed first.
Code
// An iterative process to print preorder traversal of Binary tree
void iterativePreorder(Node node)
{
// Base Case
if (node == null) {
return;
}
// Create an empty stack and push root to it
Stack<Node> nodeStack = new Stack<Node>();
nodeStack.push(root);
/* Pop all items one by one. Do following for every popped item
a) print it
b) push its right child
c) push its left child
Note that right child is pushed first so that left is processed first */
while (nodeStack.empty() == false) {
// Pop the top item from stack and print it
Node mynode = nodeStack.peek();
System.out.print(mynode.data + " ");
nodeStack.pop();
// Push right and left children of the popped node to stack
if (mynode.right != null) {
nodeStack.push(mynode.right);
}
if (mynode.left != null) {
nodeStack.push(mynode.left);
}
}
}
Space Optimized Solution:(use this as similar to in-order traversal) The idea is to start traversing the tree from the root node, and keep printing the left child while exists and simultaneously, push the right child of every node in an auxiliary stack. Once we reach a null node, pop a right child from the auxiliary stack and repeat the process while the auxiliary stack is not-empty.
Below is the implementation of the above approach:
// Iterative function to do Preorder
// traversal of the tree
void preorderIterative(Node node)
{
if (node == null)
{
return;
}
Stack<Node> st = new Stack<Node>();
// Start from root node (set curr
// node to root node)
Node curr = node;
// Run till stack is not empty or
// current is not NULL
while (curr != null || !st.isEmpty())
{
// Print left children while exist
// and keep pushing right into the
// stack.
while (curr != null)
{
System.out.print(curr.data + " ");
if (curr.right != null)
st.push(curr.right);
curr = curr.left;
}
// We reach when curr is NULL, so We
// take out a right child from stack
if (!st.isEmpty())
{
curr = st.pop();
}
}
}
Post-order traversal (Iterative)
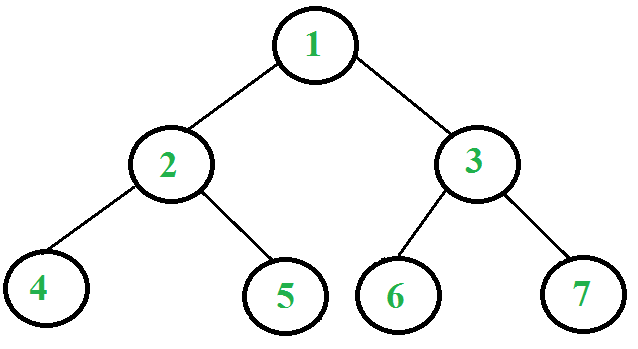
Following are the steps to print postorder traversal of the above tree using two stacks.
- Push 1 to first stack.
- First stack: 1
- Second stack: Empty
- Pop 1 from first stack and push it to second stack.
- Push left and right children of 1 to first stack
- First stack: 2, 3
- Second stack: 1
- Push left and right children of 1 to first stack
- Pop 3 from first stack and push it to second stack.
- Push left and right children of 3 to first stack
- First stack: 2, 6, 7
- Second stack: 1, 3
- Push left and right children of 3 to first stack
- Pop 7 from first stack and push it to second stack.
- First stack: 2, 6
- Second stack: 1, 3, 7, 6
- Pop 6 from first stack and push it to second stack.
- First stack: 2
- Second stack: 1, 3, 7, 6
- Pop 2 from first stack and push it to second stack.
- Push left and right children of 2 to first stack
- First stack: 4, 5
- Second stack: 1, 3, 7, 6, 2
- Push left and right children of 2 to first stack
- Pop 5 from first stack and push it to second stack.
- First stack: 4
- Second stack: 1, 3, 7, 6, 2, 5
- Pop 4 from first stack and push it to second stack.
- First stack: Empty
- Second stack: 1, 3, 7, 6, 2, 5, 4
Note- The algorithm stops here since there are no more items in the first stack. Observe that the contents of second stack are in postorder fashion. Print them.
Code
// Two stacks as used in explanation
static Stack<node> s1, s2;
static void postOrderIterative(node root)
{
// Create two stacks
s1 = new Stack<>();
s2 = new Stack<>();
if (root == null)
return;
// push root to first stack
s1.push(root);
// Run while first stack is not empty
while (!s1.isEmpty()) {
// Pop an item from s1 and push it to s2
node temp = s1.pop();
s2.push(temp);
// Push left and right children of
// removed item to s1
if (temp.left != null)
s1.push(temp.left);
if (temp.right != null)
s1.push(temp.right);
}
// Print all elements of second stack
while (!s2.isEmpty()) {
node temp = s2.pop();
System.out.print(temp.data + " ");
}
}
Using one stack solution (for post-order traversal)-
https://www.geeksforgeeks.org/iterative-postorder-traversal-using-stack/
Breadth First Search –
Approach- Iterative(over the queue i.e each node) method using Queue[Linked-list]
Algorithm
For each node, first the node is visited and then it’s child nodes are put in a FIFO queue.
printLevelorder(tree)
1) Create an empty queue q
2) temp_node = root /*start from root*/
3) Loop while temp_node is not NULL
a) print temp_node->data.
b) Enqueue temp_node’s children
(first left then right children) to q
c) Dequeue a node from q.
Implementation
// Iterative Queue based Java program
// to do level order traversal
// of Binary Tree
/* importing the inbuilt java classes
required for the program */
import java.util.Queue;
import java.util.LinkedList;
/* Class to represent Tree node */
class Node {
int data;
Node left, right;
public Node(int item) {
data = item;
left = null;
right = null;
}
}
/* Class to print Level Order Traversal */
class BinaryTree {
Node root;
/* Given a binary tree. Print
its nodes in level order
using array for implementing queue */
void printLevelOrder()
{
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
while (!queue.isEmpty())
{
/* poll() removes the present head.
For more information on poll() visit
http://www.tutorialspoint.com/java/
util/linkedlist_poll.htm */
Node tempNode = queue.poll();
System.out.print(tempNode.data + " ");
/*Enqueue left child */
if (tempNode.left != null) {
queue.add(tempNode.left);
}
/*Enqueue right child */
if (tempNode.right != null) {
queue.add(tempNode.right);
}
}
}
public static void main(String args[])
{
/* creating a binary tree and entering
the nodes */
BinaryTree tree_level = new BinaryTree();
tree_level.root = new Node(1);
tree_level.root.left = new Node(2);
tree_level.root.right = new Node(3);
tree_level.root.left.left = new Node(4);
tree_level.root.left.right = new Node(5);
System.out.println("Level order traversal
of binary tree is - ");
tree_level.printLevelOrder();
}
}
//src- g4g
Time and Space Complexity : O(n)
Approach2- Recursive
There are basically two functions in this method. One is to print all nodes at a given level (printCurrentLevel), and other is to print level order traversal of the tree (printLevelorder). printLevelorder makes use of printCurrentLevel to print nodes at all levels one by one starting from the root.
/*Function to print level order traversal of tree*/
printLevelorder(tree)
for d = 1 to height(tree)
printCurrentLevel(tree, d);
/*Function to print all nodes at a current level*/
printCurrentLevel(tree, level)
if tree is NULL then return;
if level is 1, then
print(tree->data);
else if level greater than 1, then
printCurrentLevel(tree->left, level-1);
printCurrentLevel(tree->right, level-1);