Dynamic Programming

Index

1. Introduction to Dynamic Programming
   1. Strategic Approach
   2. Common patterns
      • Top-Down Approach – recursion+memorisation
      • Bottom-up Approach – tabulation.

Introduction to Dynamic Programming

What is Dynamic Programming?

Dynamic Programming (DP) is a programming paradigm that can systematically and efficiently explore all possible solutions to a problem. As such, it is capable of solving a wide variety of problems that often have the following characteristics:

1. The problem can be broken down into “overlapping subproblems” – smaller versions of the original problem that are re-used multiple times.
2. The problem has an “optimal substructure” – an optimal solution can be formed from optimal solutions to the overlapping subproblems of the original problem.

Fibonacci Example –

If you wanted to find the n^{th}nth Fibonacci number F(n)F(n), you can break it down into smaller subproblems – find F(n – 1)F(n−1) and F(n – 2)F(n−2) instead. Then, adding the solutions to these subproblems together gives the answer to the original question, F(n – 1) + F(n – 2) = F(n)F(n−1)+F(n−2)=F(n), which means the problem has optimal substructure, since a solution F(n)F(n) to the original problem can be formed from the solutions to the subproblems. These subproblems are also overlapping – for example, we would need F(4)F(4) to calculate both F(5)F(5) and F(6)F(6).

These attributes may seem familiar to you. Greedy problems have optimal substructure, but not overlapping subproblems. Divide and conquer algorithms break a problem into subproblems, but these subproblems are not overlapping (which is why DP and divide and conquer are commonly mistaken for one another).

There are two ways to implement a DP algorithm:

1. Bottom-up, also known as tabulation.
2. Top-down, also known as memoization.

Bottom-up (Tabulation)

Bottom-up is implemented with iteration and starts at the base cases. Let’s use the Fibonacci sequence as an example again. The base cases for the Fibonacci sequence are F(0)=0 and F(1) = 1. With bottom-up, we would use these base cases to calculate F(2)F(2), and then use that result to calculate F(3), and so on all the way up to F(n)

Pseudi COde

// Pseudocode example for bottom-up

F = array of length (n + 1)
F[0] = 0
F[1] = 1
for i from 2 to n:
    F[i] = F[i - 1] + F[i - 2]

Top-down (Memoization)

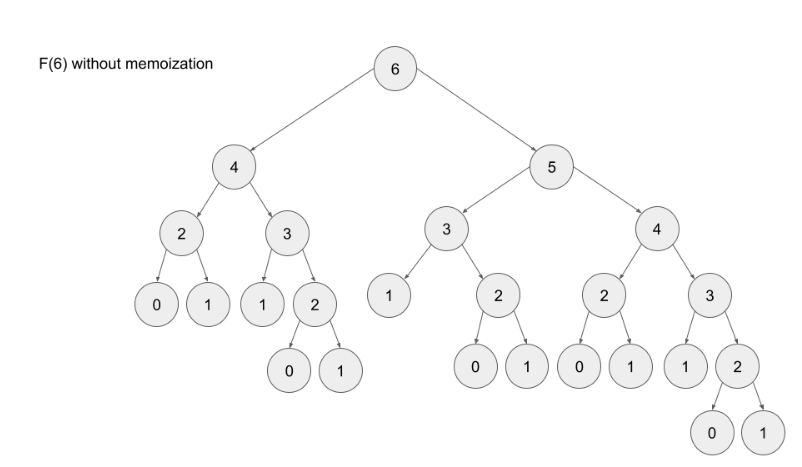
Top-down is implemented with recursion and made efficient with memoization. If we wanted to find the n^{th}nth Fibonacci number F(n)F(n), we try to compute this by finding F(n – 1)F(n−1) and F(n – 2)F(n−2). This defines a recursive pattern that will continue on until we reach the base cases F(0) = F(1) = 1F(0)=F(1)=1. The problem with just implementing it recursively is that there is a ton of unnecessary repeated computation. Take a look at the recursion tree if we were to find F(5)F(5):

Notice that we need to calculate F(2) three times. This might not seem like a big deal, but if we were to calculate F(6), this entire image would be only one child of the root. Imagine if we wanted to find F(100) – the amount of computation is exponential and will quickly explode. The solution to this is to memoize results.

Note- memoizing a result means to store the result of a function call, usually in a hashmap or an array, so that when the same function call is made again, we can simply return the memoized result instead of recalculating the result.

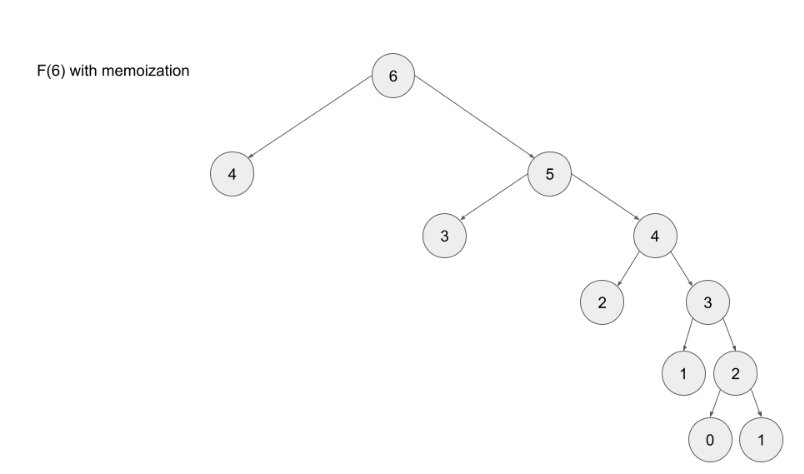
Advantages

• It is very easy to understand and implement.
• It solves the subproblems only when it is required.
• It is easy to debug.

Disadvantages

• It uses the recursion technique that occupies more memory in the call stack.
• Sometimes when the recursion is too deep, the stack overflow condition will occur.
• It occupies more memory that degrades the overall performance.

When to Use DP

Following are the scenarios to use DP-

1. The problem can be broken down into “overlapping subproblems” – smaller versions of the original problem that are re-used multiple times
2. The problem has an “optimal substructure” – an optimal solution can be formed from optimal solutions to the overlapping subproblems of the original problem.

Unfortunately, it is hard to identify when a problem fits into these definitions. Instead, let’s discuss some common characteristics of DP problems that are easy to identify.

The first characteristic that is common in DP problems is that the problem will ask for the optimum value (maximum or minimum) of something, or the number of ways there are to do something. For example:

• Optimization problems.
  • What is the minimum cost of doing…
  • What is the maximum profit from…
  • How many ways are there to do…
  • What is the longest possible…
  • Is it possible to reach a certain point…
• Combinatorial problems.
  • given a number N, you’ve to find the number of different ways to write it as the sum of 1, 3 and 4.

Note: Not all DP problems follow this format, and not all problems that follow these formats should be solved using DP. However, these formats are very common for DP problems and are generally a hint that you should consider using dynamic programming.

When it comes to identifying if a problem should be solved with DP, this first characteristic is not sufficient. Sometimes, a problem in this format (asking for the max/min/longest etc.) is meant to be solved with a greedy algorithm. The next characteristic will help us determine whether a problem should be solved using a greedy algorithm or dynamic programming.

The second characteristic that is common in DP problems is that future “decisions” depend on earlier decisions. Deciding to do something at one step may affect the ability to do something in a later step. This characteristic is what makes a greedy algorithm invalid for a DP problem – we need to factor in results from previous decisions.

Algorithm –

You can either use Map or array to store/memoize the elements (both gives O(1) access time.