Author: sevanand yadav

software engineer working as web developer having specialization in spring MVC with mysql,hibernate

Security Intro

Objective –

  1. meaning /structure of security mechanism
  2. where used? use case
  3. Implementation

Index

  1. Introduction
  2. Basic username-pwd
  3. JWT
  4. Oauth ( micro-services)
  5. Digital Signature (NPCI)

Introduction

Session, Cookie, JWT, Token, SSO, and OAuth 2.0 – here’s what you need to know

These terms are essential for identifying, authenticating, and authorizing users online. Let’s dive in👇

𝗪𝗪𝗪-𝗔𝘂𝘁𝗵𝗲𝗻𝘁𝗶𝗰𝗮𝘁𝗲
🔹 Oldest & most basic method
🔹 Browser asks for username & password
🔹 Lacks control over login life cycle
🔹 Rarely used today

𝗦𝗲𝘀𝘀𝗶𝗼𝗻-𝗖𝗼𝗼𝗸𝗶𝗲
🔹 Server maintains session storage
🔹 Browser keeps session ID
🔹 Works mainly with browsers, not mobile app friendly

𝗧𝗼𝗸𝗲𝗻
🔹 Compatible with mobile apps
🔹 Client sends token to server for validation

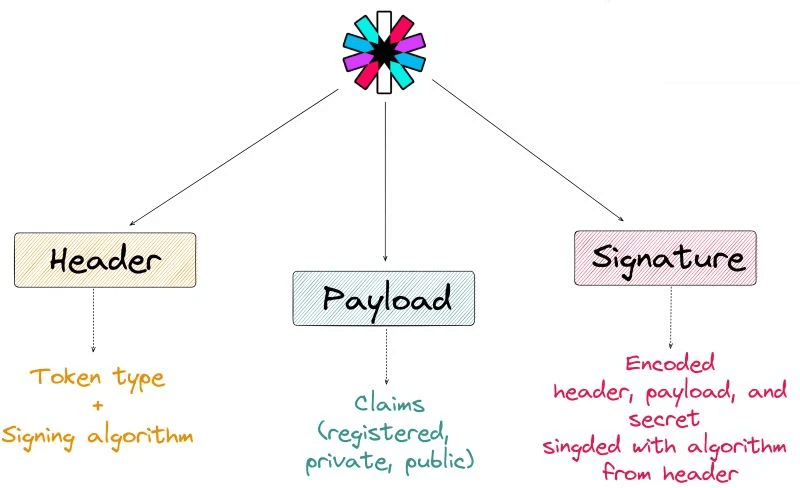
𝗝𝗪𝗧 (𝗝𝗦𝗢𝗡 𝗪𝗲𝗯 𝗧𝗼𝗸𝗲𝗻)
🔹 Standard representation of tokens
🔹 Digitally signed & verifiable
🔹 No need to save session info server-side

𝗦𝗦𝗢 (𝗦𝗶𝗻𝗴𝗹𝗲 𝗦𝗶𝗴𝗻-𝗢𝗻) & 𝗢𝗔𝘂𝘁𝗵 𝟮.𝟬
🔹 SSO: Log in once, access multiple sites
🔹 Uses CAS (central authentication service)
🔹 OAuth 2.0: Authorize one site to access info on another

JWT

Index

  1. What is JWT?
  2. When to use and why?
  3. Application

𝗪𝗵𝗮𝘁 𝗶𝘀 𝗝𝗪𝗧?

Securing the API is one of the most important things to do to prevent its abuse. It is done via the authentication and authorisation process and the most used is the 𝗝𝗪𝗧 token-based mechanism.

JSON Web Token is a standard that is used to share information between client and server as a JSON object.

Official Introduction- https://jwt.io/introduction

It is represented as a string that consists of 3 parts: (Memory map JWT[3words 3 parts – H.P.S. – Header Payload Signature])

  1. 𝗛𝗲𝗮𝗱𝗲𝗿: It consists of token type(typ) and signing algorithm that is used(alg). The type will always be JWT, and the signing algorithm can be HMAC SHA256 or RSA.
  2. 𝗣𝗮𝘆𝗹𝗼𝗮𝗱: This part contains related data(mostly for users) known as claims. There are three types of claims:
    • 𝗥𝗲𝗴𝗶𝘀𝘁𝗲𝗿𝗲𝗱 – claims that are recommended to use for interoperability like issuer(iss), subject(sub), expiration time(exp), etc.
    • 𝗣𝘂𝗯𝗹𝗶𝗰 – contains generic information like email, name, or role. It’s recommended to use collision-resistant names to avoid collision with private claims.
    • 𝗣𝗿𝗶𝘃𝗮𝘁𝗲 – custom claims
  3. 𝗦𝗶𝗴𝗻𝗮𝘁𝘂𝗿𝗲: It ensures that the token hasn’t been altered. JWT is signed with the algorithm from a header, and the signature consists of an encoded header and payload, and secret.

A string is always encoded like a Base64 string where every part is separated by dots and like that is easily passed in HTTP environments through HTTP headers.

Note:

  1. the claim names are only three characters long as JWT is meant to be compact.
  2. though signed tokens are protected against tampering, is readable by anyone(base-64 decry-pt). Do not put secret information in the payload or header elements of a JWT unless it is encrypted. (Note – the token is encoded not encrypted)

Relevant articles on encryption vs encoding

Where JWT Is used? (refer official link above for description)

  1. Authorisation
  2. Information exchange

When to use and why?

In cases of S2S cases, no needed to maintain additional tokens for 3rd party.

Application

Artificial Intelligence

AI tools that gives you superpowers and save countless hours!

(Multi)media generation/modification

  1. 🎧 Krisp: Enjoy peaceful calls with AI that removes background noise. https://krisp.ai/
  2. 🎵 Beatoven: Create unique, royalty-free music. https://www.beatoven.ai/
  3. 🎙️ Cleanvoice: Edit podcast episodes automatically. https://cleanvoice.ai/
  4. 🎤 Podcastle: Studio-quality recording from your computer. https://podcastle.ai/
  5. Video

Content generation

  1. 📸 Stockimg: Find the perfect stock photo every time. https://stockimg.ai/

Professional use tools

  1. Emails
  2. Resume
  3. Meetings

Miscellaneous

🤖 theresanaiforthat: A comprehensive database of AI tools for every task. https://lnkd.in/dKhqaaF3

——————————————————————

Junit and Mocking and spy

Index

  • Junit
  • Mockito
  • testing private method (reflection ,powermock)

2 testing fameworks- MOckito abd Sping testing

MOckMOckBean
annotationpary of MockitoframeworkSPring testing framework
framework@RunWith(MockitoJUnitRunner.class) public class MyServiceTest { @Mock private MyRepository myRepository;@SpringBootTest public class MyServiceIntegrationTest { @Autowired private MyService myService; @MockBean private MyRepository myRepository;
PurposeUnitTetsingIntegration testing

Spy vs Mock

@spy@Mock
FunctionalityA partially mocked version of a real object.A complete replacement for a real object.
CreationWraps an existing objectCreates a new object
ControlPartial control (can define specific behaviors for specific methods)Full control over behavior
Use caseTesting interactions within a real object with some real behaviorIsolating dependencies, unit testing with specific behavior
accesscan access private methods of the original objectcannot access private methods of the original object
examplebelow codebelow code //

Mock usage

// Interface we want to test
public interface EmailService {
  void sendEmail(String recipient, String message);
}

// Test class using mock
@Test
public void testSendEmail() {
  // Create a mock object of EmailService
  EmailService mockEmailService = Mockito.mock(EmailService.class);

  // Define behavior for the mock object
  Mockito.when(mockEmailService.sendEmail("user@example.com", "Hello world!")).thenReturn(true);

  // Use the mock object in your test logic
  myService.sendNotification(mockEmailService, "user@example.com", "Hello world!");

  // Verify interactions with the mock object
  Mockito.verify(mockEmailService).sendEmail("user@example.com", "Hello world!");
}

IN above example :

  • We create a mock object of EmailService using Mockito.mock.
  • We define behavior for the sendEmail method using Mockito.when. Here, it always returns true.
  • We use the mock object in the test and verify its interaction later.

Spy usage

// Real implementation of EmailService
public class RealEmailService implements EmailService {
  @Override
  public void sendEmail(String recipient, String message) {
    // Send email logic goes here (not shown for simplicity)
  }
}

// Test class using spy
@Test
public void testSendEmailWithSpy() {
  // Create a real object
  EmailService realEmailService = new RealEmailService();

  // Create a spy object from the real object
  EmailService spyEmailService = Mockito.spy(realEmailService);

  // Define behavior for specific method (optional)
  Mockito.when(spyEmailService.sendEmail("admin@example.com", "Alert!")).thenReturn("Sent successfully");

  // Use the spy object in your test logic
  myService.sendNotification(spyEmailService, "user@example.com", "Hello world!");
  myService.sendNotification(spyEmailService, "admin@example.com", "Alert!");

  // Verify interactions (optional)
  Mockito.verify(spyEmailService, times(2)).sendEmail(anyString(), anyString());
}

IN above example :

  • Create a real RealEmailService object.
  • Create a spy of the RealEmailService using Mockito.spy.
  • Define behavior for the sendEmail method to return a specific message for “admin@example.com” email.
  • Use the spy object and verify interactions (optional).

		<dependency>
			<groupId>org.powermock</groupId>
			<artifactId>powermock-module-junit4</artifactId>
			<version>1.7.4</version>
		</dependency>

https://www.learnbestcoding.com/post/21/unit-test-private-methods-and-classes

REfernce

https://www.tutorialspoint.com/mockito/mockito_spying.htm

Quartz

Quartz provides a way to schedule the recurring execution of job.

Important Points

  • Quartz differentiates between Job (What/Task) and Trigger (when) – so both appear as different statement
  • Two types pf scheduling- simple and cron based.
  • Quartz related properties related to cron and others are usually kept in quartz.properties

Cron expression and their meaning-

  1. http://www.quartz-scheduler.org/documentation/quartz-2.3.0/tutorials/crontrigger.html

Questions –

Configuration – number of thread pool size.

Asymptotic Analysis and notation

Index

  1. Time Complexity
  2. Common DS Operations Time Complexity and Space Complexity

Time-complexity

Big-O notation: 𝑂O

It describes the asymptotic upper bound, the worst case of time complexity. i.e the max number of times a statement executes. 

Measurement of time complexity

  1. O(N) Linear TC – When the number of operation growth is proportional to input i.e same number of operation as the input size then it’s Linear TC
  2. O(N^2) – Quadratic Algorithm TC
  3. O(LogN) -when algorithm decreases the input data in each step
    • Example Binary search
  4. O(2^n) – opeation doubles with each increment in input data.

Growth Order

O(n!) > O(2 ^n) > O(n^3) > O(n^2) > O(nlogn) > O(n) > O(Log N) > O(sqrt(N)) > 1

Graph

Index

  1. Introduction
  2. Dijkstra Algorithm
  3. Bellman-ford Algorithm
  4. Floyd-Warshall Algorithm
  5. Prim’s Algorithm

Introduction

Common Terminology –

  1. Minimum Spanning Tree (MST) used in prims algorithm
    • Goal: To connect all vertices in a graph with the minimum possible total edge weight, without forming any cycles.
    • Output: A tree that spans all vertices of the graph with the minimum sum of edge weights.
  2. Shortest path
    • Goal: To find the shortest path between a specific pair of vertices in a graph, minimizing the sum of the edge weights along that path.
    • Output: A path (which may include some or all vertices) with the minimum possible total weight between two specific vertices.

Dijkstra Algorithm

  1. Purpose: Finds the shortest path from a single source to all other vertices in a graph.
  2. Applicability: Works only with graphs that have non-negative edge weights.
  3. Woking:
    • Uses a greedy approach.
    • Iteratively selects the vertex with the smallest known distance, explores its neighbors, and updates their distances.
    • Once a vertex is processed, its shortest path is finalised.

Dijkstra’s algorithm is like breadth-first search  (BFS), except we use a priority queue  instead of a normal first-in-first-out queue.  Each item’s priority is the cost of reaching it.

Note-Implementation is similar to Prim’s algorithm for minimum spanning tree.

REf-

  1. https://www.interviewcake.com/concept/java/dijkstras-algorithm (desciption working in chart)
  2. https://www.tutorialcup.com/interview/algorithm/dijkstra-algorithm.htm (application + short implemntation)
  3. https://www.interviewbit.com/tutorial/dijkstra-algorithm/ (Pseudo code + Graph Algo)
    1. https://www.interviewbit.com/tutorial/breadth-first-search/#breadth-first-search

Bellman-Ford Algorithm

  1. Purpose: Also finds the shortest path from a single source to all other vertices, but can handle graphs with negative edge weights.
  2. Applicability: Works with graphs that may have negative edge weights, and can also detect negative weight cycles (where a cycle’s total weight is negative).
  3. Woking:
    • Uses a dynamic programming approach.
    • Iteratively relaxes all edges, meaning it updates the shortest path estimate for each edge based on its current known distance.
    • After V−1V-1V−1 iterations, it ensures that the shortest paths are found. If an additional relaxation improves any distance, it indicates a negative weight cycle.

Floyd-Warshall Algorithm

  1. Purpose: Finds the shortest paths between all pairs of vertices in a graph.
  2. Applicability: Works with both directed and undirected graphs, including those with negative edge weights.
  3. Wokings:
    • Uses a dynamic programming approach.
    • Iteratively updates a distance matrix where each entry dist[i][j] represents the shortest path from vertex i to vertex j.
    • Considers each vertex as an intermediate point in the path and updates the matrix accordingly.

Prim’s Algorithm

  1. Purpose: Finds the Minimum Spanning Tree (MST) of a connected, undirected graph. The MST is a subset of the edges that connects all vertices together, without any cycles, and with the minimum possible total edge weight.
  2. Applicability: Works with weighted, undirected graphs. It requires that the graph be connected, meaning there must be a path between every pair of vertices.

Arrays Algorithms

  1. Boyer-Moore Majority Voting Algorithm
  2. Kadane’s Algo

Boyer-Moore Majority Voting Algorithm

A majority element is one that appears more than nums.length / 2 times.

Algorithm Proceeding-

  1. First, choose a candidate from the given set of elements
  2. if it is the same as the candidate element, increase the votes. Otherwise,
    • decrease the votes if votes become 0, select another new element as the new candidate.
public static int findMajorityElement(int[] nums) {
        int majorityElement = 0;
        int count = 0;
        
        for (int num : nums) {
            if (count == 0) {
                majorityElement = num;
                count = 1;
            } else if (num == majorityElement) {
                count++;
            } else {
                count--;
            }
        }
}

Kadane’s Algo

Kadane’s algorithm a popular dynamic programming algorithm, it is used for finding the maximum sum of a contiguous subarray in an array. it efficiently handles both positive and negative numbers.

Conditions/Cases to remember

  • does it handle empty array?[NA]
  • does it handle all -ve element, i.e what will be the ans in this case, since sum of 2 -ve is grater -ve number. [YES]
  • should we consider using 0 or arr[i] as substitution in code – Any works ,but corresponding initiation & iteration required.

It works by maintaining two variables:maxSoFar & maxEndingHere

  1. maxSoFar stores the maximum sum of any contiguous subarray seen so far, and
  2. maxEndingHere stores the maximum sum of any contiguous subarray ending at the current index.
public static int maxSubArraySum(int[] nums) {
int maxSoFar=Integer.MIN_VALUE;//final result initiated to min not 0, for cases where elements with -ve numbers would result in max being 0 -which is incorrect.
        int maxEndingHere=0;
        for(int i=0;i<nums.length;i++){
            maxEndingHere=Math.max(nums[i]+maxEndingHere,nums[i]);
            maxSoFar=Math.max(maxSoFar,maxEndingHere);
        }
      return maxSoFar;  
}